

Almost nothing at all is known about the nature of Harmony.
Music Theory, as a field, has failed to offer up any profound truths about Harmony. The various systems which music theorists have constructed, from the Ars Noveau of the Middle ages to the modern Neo-Reimannian theories, are little more than superficial classification systems. Harmony categorized into modes, Harmony categorized into Reimannian functions, Harmony categorized into Lewinian transformations - none of these reveal anything about the underlying nature of Harmony; they only succeed in taking the musical styles of the greatest composers and in reducing them to systems which can be taught, imitated, endlessly reproduced. They are not so much meant to help us understand Harmony as they are meant to help us wield it. They are not truthful, but practical.
It is almost universally agreed upon among Western musicians that there is some harmonic quality called Consonance and an opposing quality called Dissonance; and yet, there seems to be almost no useful discussion regarding the deeper nature of these two qualities. Nowhere else, more than here, is the stagnancy of music theory made more apparent. Despite the great attention we have given this subject and despite all of our great advancements in acoustical science, we are no closer now to a clear understanding of the phenomenon of Consonance than we were in the Middle Ages. But this, reader, should tell us that the problem lies not with the sum of our knowledge, but in our underlying premises...
Music theory is currently dominated by a conception of Harmony which originates in the Pythagoreans, and which can be summarized in the following way:
"An interval is more consonant the more numerically simple it is."
In music, an "interval" describes the relationship between two pitches, usually in the form of a ratio. A pitch at 400 Hz and a pitch at 300 Hz, for instance, create the interval of 4/3. A pitch at 900 Hz and a pitch at 800 Hz create the interval of 9/8. According to the Pythagorean conception of Harmony, the former is more consonant than the latter because the ratio between its two pitches is simpler.
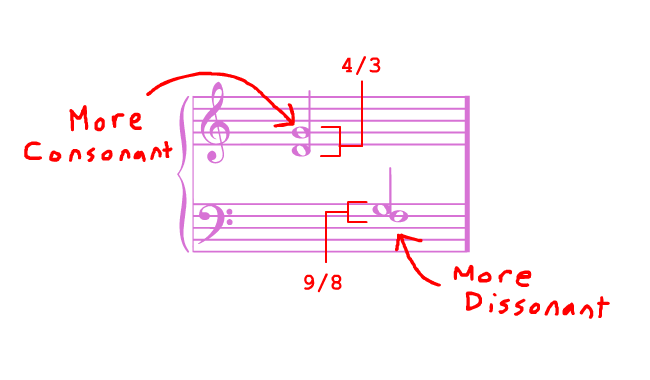
What plagues our understanding of Harmony more than anything else is how deeply we have internalized the Pythagorean system. The primary claim - the supposed equivalence between consonance and numerical simplicity - is easily refuted. What is really damaging to our theory is not this superficial claim, but its underlying premise: the idea that intervals are the source of consonance. This premise goes totally unquestioned by music theorists.
Read through the Harmonic Treatises of Zarlino, Rameau, Reimann, Schenker, and Partch. One will find that the same method used in all of them. First he lists off a set of INTERVAL-RATIOS. Only once he has finished appraising each of these intervals as some level of consonant or dissonant does he then feel comfortable using them to reconstruct the classical scales and chords which he is used to. It is so obvious to him that this is the correct order of operations - that the INTERVAL must come first and everything else second.

Our preoccupation with intervals has only become stronger in the modern strains of theory. With the old European traditions and systems torn away, the modern theorist has to lean further into the core of the Pythagorean doctrine, which is all he has left to go off of. This is why Harry Partch, supposedly a revolutionary theorist, merely restates the 2500-year-old Pythagorean conception. Partch rebels against the "outdated" Western doctrines of Harmony, but in its place he can only provide the far older doctrines of the Greeks. Look at the modern Consonance-Dissonance maps: the Plompt-Levelt curve, Partch's "One-Footed Bride." They both map Consonance and Dissonance levels onto INTERVALS.

In all of these Harmonic systems the interval is assumed to be the source of Consonance. To music theorists, it is never the harmonic-structure ITSELF which is viewed as Consonant, but rather the intervals which it consists of. A major triad is not consonant; the 5/4 and the 6/5 within it are. The harmonic series is not consonant; just the intervals within it. Harmony essentially only takes place at the level of the interval, and the broader harmonic structures we have built - the chords, the scales, the songs - are merely sets of intervals shoved together.
So, all music theorists have, without knowing it, been Pythagorean music theorists. They have blindly adopted Pythagoras' hopelessly narrow conception of Harmony - one in which intervals are the essence of all Harmony and everything else is derived after the fact. It is indicative of the weakness of music theorists that none of them have even questioned the existence of a "consonant interval." Who are we to say that the interval, itself, is the thing that is consonant? What if it is only the broader harmonic structure which is consonant, and the intervals are merely fragments of this broader structure? Perhaps every interval is truly worthless without the context of the broader harmonic structure, and every attempt to view the interval as such as an indication of consonance has doomed our theory from the start? If we are to make any headway in the field of music theory, such alternatives absolutely mustbe considered.
I think it is about time we move beyond the work of the Greeks. It matters little how widely our conclusions about Consonance vary, if they are always restricted from the very outset by assumptions which were made 2500 years ago. We must broaden our vision of Harmony and of music as a whole. The problems which confront music theory demand it.
The rigid and boring character of Western music theory begins to make sense when we consider these rocky origins. The kernel of Pythagoras' philosophy was this: "the essence of all things is number." It needs to be understood that Pythagoras' music theory was nothing more than an extension of this philosophy. Intervals are ratios, and ratios are numbers. In Pythagoras' purely intervallic music theory, number becomes the sole basis of Harmony; music itself is reframed as "numbers given sound," as the actualization of the ideas of mathematics through the sense-world of the ear. This is the conception of music which was put forth by Pythagoras and that which every music theorist since has unconsciously adopted. Like every truly great philosopher, Pythagoras' innermost desire was not to understand the world, but to enslave it to his own philosophy. Philosophers are conquerers. And nowhere in the entire history of philosophy do we find a greater conquest than in this complete subjugation of music to Pythagoras' number-philosophy. Even now, one still always hears it said that "music is math."
Of all the arts, only music has been subject to such a hyper-numerical treatment. When we look at a beautiful painting, like Rembrandt's "Night Watch," are we, at the bottom of it, just perceiving some mathematically perfect object - some formula or function which rendered into visual image? Absolutely not! The qualities which define the work - its colors, shapes, light, dark, shading, depth, framing, etc. - are all qualities particular to our sense of sight, qualities which cannot be reduced to mere number. Certainly, one could measure out some set of lengths in this painting, and one could argue that their "simple proportion" contributes, in some subtle way, to the piece's beauty, but only an absolute fool would claim that the entirety of the piece's aesthetic value rests on these proportions. But this is the exact treatment we have given music!
Compare the language of music theory with the language with which we describe other sensory phenomena. Our language for describing smells and tastes is almost entirely based on analogy: "fruitty," "nutty," "earthy," "salty," "spicy," - every one of these descriptors invokes an association with some actual sensual experience. Sight is described almost entirely in terms of colors, shades, and light - qualities which are specific only to that sense-world and which cannot be constrained by numbers. Etymology suggests that our words for colors, as well, originated in references to actual visual objects. Green shares roots with "grass" and "grow", yellow with "glow" and "gold," red with "reed" and "ruby" and "rhubarb." Our language for describing Harmony lacks this kind of straightforward connection to the senses. Words such as "voice-like," "buzz-like," "howl-like," "chirp-like," "scream-like," "whisper-like," and "hum-like" are entirely absent from music theory, even though they would probably reveal far more about the meaning of a given harmony than the conventional "this chord consists of a 5/4, 5/3, 4/3, and 2/1."
Music viewed in this way takes on an infinitely abstract character. Where other art forms like theatre, dance, and painting are viewed as sensuous, orgiastic, and intertwined with life itself, music is thought to be as abstract, cold, and logical as the numbers which supposedly make it up. And here, precisely, is the "value" of Pythagorean Harmony; here is why it gained such a universal appeal and why it has continued to go unquestioned for thousands of years: such a cold and sterile answer to the problem of Harmony appeals to the very cold and sterile type of person that is most likely to study Harmony - that is, the academic dork. The dork loves numbers; he wraps up the world in his numbers; he tries his best to conceive of everything as numerical. He would turn the whole world into a formula, in much the same way that an ant, if allowed to, would turn the whole world into one giant anthill. Numbers are comfortable and sterile and, best of all, they seem to bear the stamp of "objectivity." The crudest and most mediocre type of academic always believes that the moment something can be rephrased numerically it has finally been "figured out." Why is Harmony beautiful? "Because we're like... hearing numbers." What is so beautiful about the numbers? "Ummm, they just ARE, okay?!!"
So the Pythagorean conception of Harmony is to blame for the sterility of our field. By framing Harmony as something purely numerical, it has completely separated our understanding of Harmony from our basic sensuous impressions. It seems to me that this is why music theory has made so little headway: its unquestioned premises are the issue.
In this blog, our goal will be to develop a theory of Consonance which has its basis, not in numbers, but in actual sounds. We reject the Pythagorean view of Harmony which, by its callous reduction of Harmony to a purely numerical form, has distorted our impressions of music so that the average person ocan only think of it as an artform dominated by logic, patterns, and measurements. In contrast to this Pythagorean conception, we view music to be illogical, strange, and amorphous. Every numerical representation of Harmony, therefore, will be treated with the utmost suspicion. We take music for what it is: an artform thoroughly rooted in our sense of sound and which cannot be understood outside of that particular sense-world. Every attempt will be made to understand harmonies by drawing analogies between them and other sounds. In this way, we hope to re-establish the connection between our music theory and our basic sense-perceptions which has long been severed.
All sound is made up of frequencies, oscillations of air pressure over time. Frequencies should be regarded as atomistic to the world of sound, in that they are the indivisible sound particles which by themselves mean little but out of which every sound can be produced. Accordingly, to say that the sound-world is “just a bunch of frequencies” would be a reduction as shallow and useless as saying that the physical world is “just a bunch of atoms.”
What matters is clearly not the frequency-atoms themselves, but the shapes which are made when they combine together; and from the infinite set of these shapes, I distinguish between two fundamental types: Tone and Noise.
A tone is a sound which is made of many frequencies but is only heard as one pitch. Noise is a sound which is composed of many frequencies but is heard without pitch.
The distinction I make between frequency and pitch, here, may confuse some readers, as the two terms are almost always used interchangeably. Conventionally, it is understood that a physical frequency at 400 Hz will be perceived by the listener to be at the pitch of 400 Hz, end of story. But this fact only applies to frequencies in isolation. When we hear multiple frequencies at once, there is almost always a disparity between the actual number of frequencies, and the number of pitches we perceive in them. This disparity is most clearly exemplified in Tone and Noise.
This is the frequency spectrum of the sound produced when a C3-note on a piano is played:
This is a tone. We have multiple frequencies playing simultaneously, but rather than hearing many pitches, as one might expect, we only hear one. Every tone that we hear, whether its source is a piano, violin, human-voice, didgeridoo, bird-call, or trumpet, is, like the tone above, a collection of frequencies which combines together to create a single pitch. This is a fact which often suprises the uninitiated into acoustics, because the pitch created by the set of frequencies is so absolute and so pure.
On the other hand, here is the frequency spectrum of the sound produced by a cymbal crash:
This is a noise. Once again, we have multiple frequencies playing simultaneously, but this time we do not perceive any single pitch; rather, we perceive a general range of pitchless sound.
So, in these two fundamental sound-types the distinction between "frequency" and "pitch" is made clear: frequencies are the physical components which make up every sound, but pitch is a feeling resulting from the arrangement of these frequencies. Going forward, the reader will find that much of Harmony depends on this unequal relationship between pitch and frequency.
And so, keeping in mind the distinction between frequency and pitch, we can begin to understand the first of our two types of sound: Noise.
Noise is sound-without-pitch. If we hear a frequency in isolation, we register it as a pitch, as a single "point" in acoustical space. But the more frequencies we hear simultaneously, the more difficult it becomes to identify them as individual pitch-points. Put simply: the more frequencies we hear, the more they "clutter" our range of hearing.
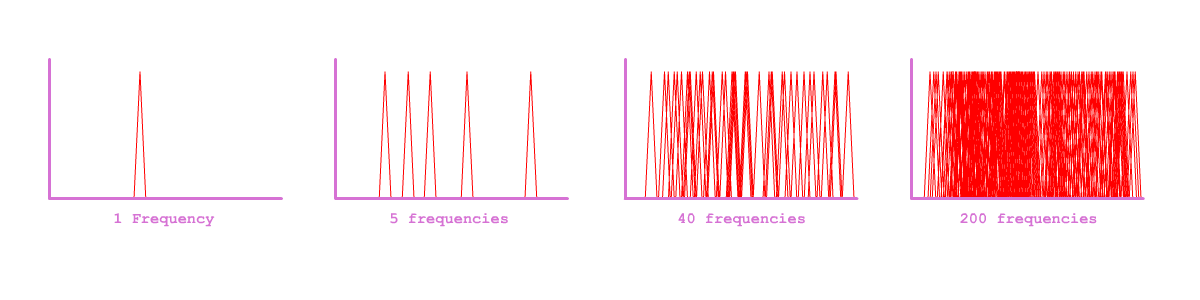
At some point, we cease to register individual pitches at all, instead perceiving the range which they occupy. This is roughly where a sound becomes a NOISE. Just as we would perceive thousands of grains of sand not individually but as a single homogenous substance, so too do we experience thousands of frequencies not individually but as a single, homogeneous noise. A "Sound-mass."
"Brown" noise (frequencies occupying the lower range of human hearing):
"White" noise (frequencies occupying the full range of human hearing):
"Purple" noise (frequencies occupying the higher range of human hearing):
Noises are defined by the density and range of their frequencies. They are "sound-as-mass." Just a rudimentary clashing together of many sounds without regard for placement.
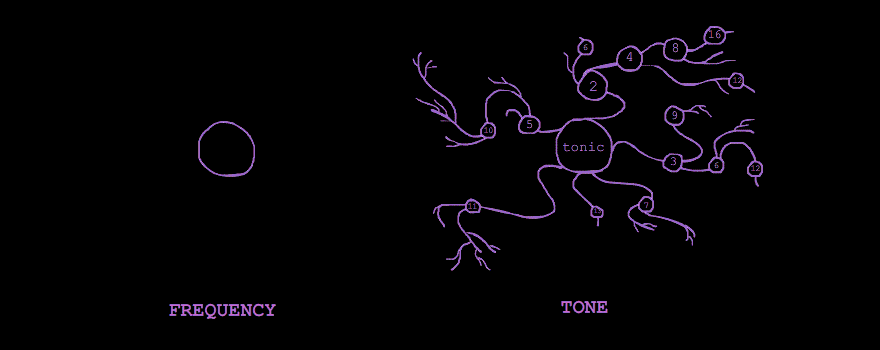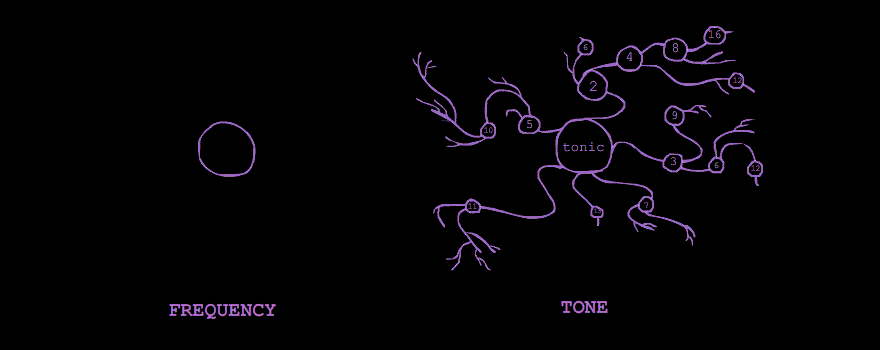
Noise represents a general rule of sound: that the more frequencies we hear simultaneously, the more these frequencies obscure each other. The one exception to this rule is the sound which I call the Tone. The Tone's frequencies fall into a structure which allows them to compound them into a singular feeling of pitch. This structure is the Harmonic Series.
The Harmonic Series - sometimes called the "overtone series" - is a series of frequencies naturally created by the resonations of a physical body. If a piano-string, for instance, begins to vibrate at a certain frequency, that frequency will not only travel through the air but through the rest of the piano, reverberating through its body and its other strings. By these reverberations, a series of resonant frequencies, or harmonics is produced. These harmonics will all be multiples of the initial frequency, or the tonic. If the tonic is 100 Hz, for instance, a series of harmonics will be produced at 200 Hz, 300 Hz, 400 Hz, 500 Hz, and so on.
This naturally occuring series of frequencies is called The Harmonic Series. It is the imperceptible structure hidden within every tone we hear - every trumpet-sound, every bird-chirp, every voice.
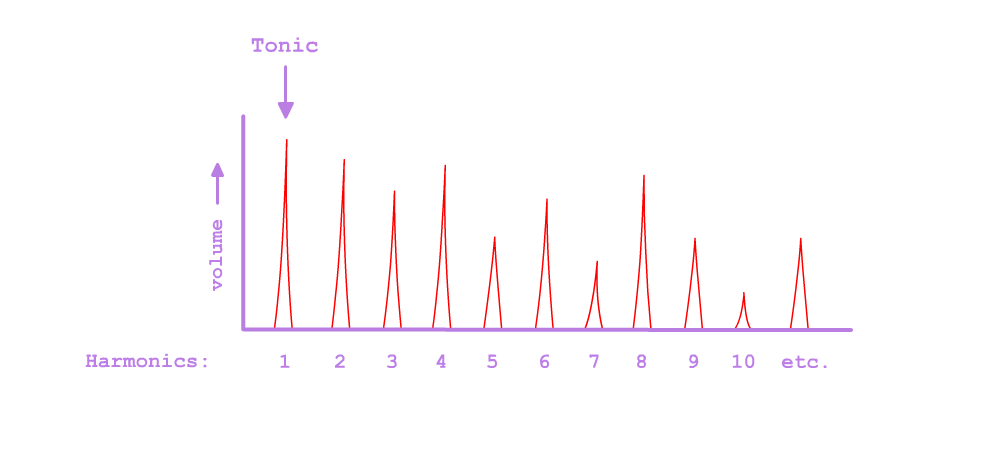
It must be understood from the outset that a tone is made up of its harmonics. A tone does not have a harmonic series; it is a harmonic series. Too often, music theorists treat the harmonic series as something tacked onto a tone; only its pitch is seen as important, while the rainbow of various harmonics is treated as more-or-less arbitrary. Nothing could be further from the truth!
There is a world of difference between a frequency at 440 Hz and a tone at 440 Hz.
This is a single frequency in isolation:
But THIS is a tone:
Both are heard as a single pitch, but the latter has DEPTH! While the frequency is just an acoustical "atom," the Tone is an elaborate acoustical molecule, one in which many interrelated harmonics contribute to a single over-arching feeling of sound.
So, the Tone is far more than just a pitch-class; it is, itself, a harmony.
The Tone is an anti-Noise. Whereas a noise is merely a group of disparate frequencies, the tone is a unified body. Every frequency within a single tone assimilates into the same pitch. Noise is the "default" state of sound because it is natural for separate frequencies to have separate pitches, pitches which necessarily detract from each other. But in the Tone, every harmonic forgoes its own pitch-feeling, assimilating, rather, into the over-arching pitch established by the tonic. Rather than a cloud of disparate frequency-particles, we get a constellation of various harmonic identities which all act as differet extensions of the tonic - as unique accentuations of its pitch-feeling.
In this way
Here, also, the plurality of harmonic identities in the Tone is something entirely different from the Noise's grey homogeneity. It is only by their common relation to a singular tonic that the harmonics are able to differentiate from each other. As separate frequencies each harmonic means nothing, but in relation to the tonic they all have separate harmonic feelings.
Noise and Tone represent the furthest extremes of sound. The former is acoustical mass while the latter is harmonic structure. The former is defined by the density and range of its frequencies, while the latter is defined by their position and volume. Here, we get an acoustical duality as sharp as that between dark and light.
These two fundamental sounds, Tone and Noise, represent the furthest extremes of Harmony. The Tone is one-pitched sound; Noise is sound-without-pitch. Sound-as-structure and sound-as-mass. 1 and 0. Form and unform. The whole of our acoustical experience rests upon our distinction between these two extremes.
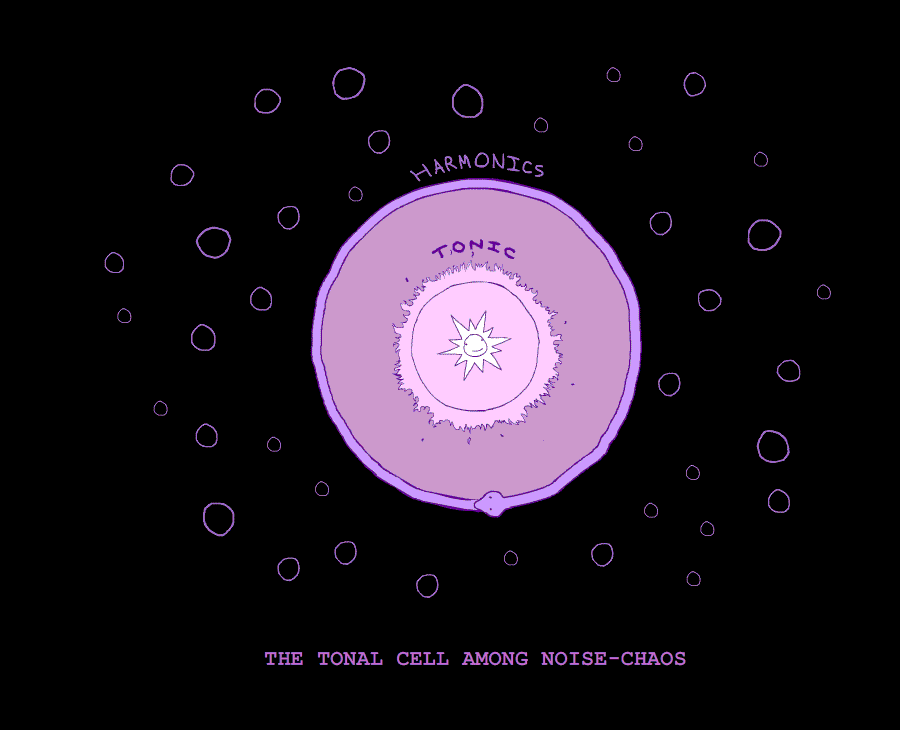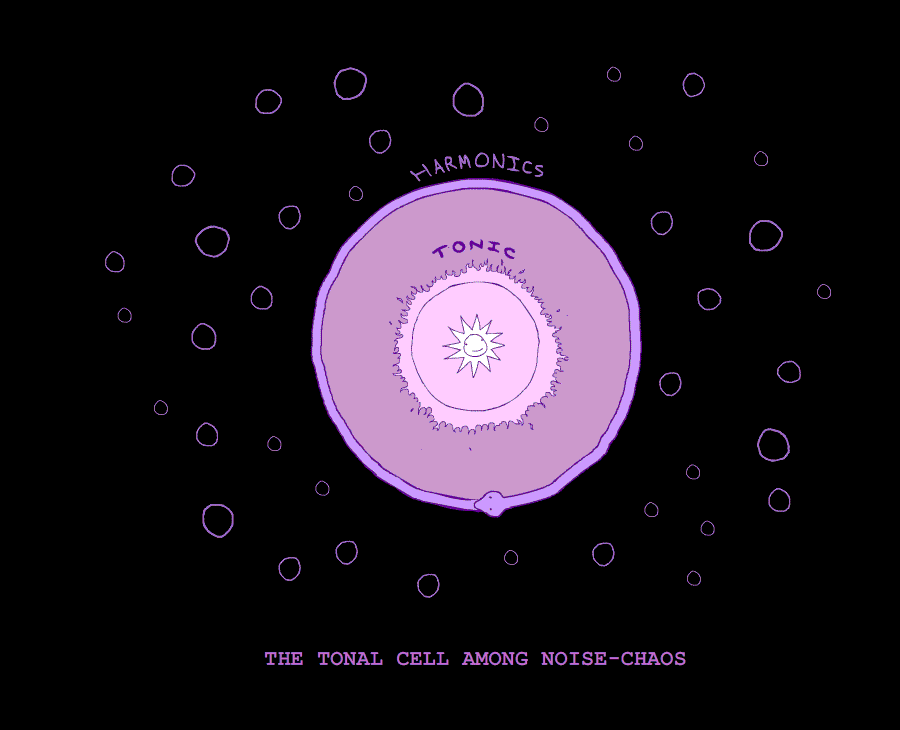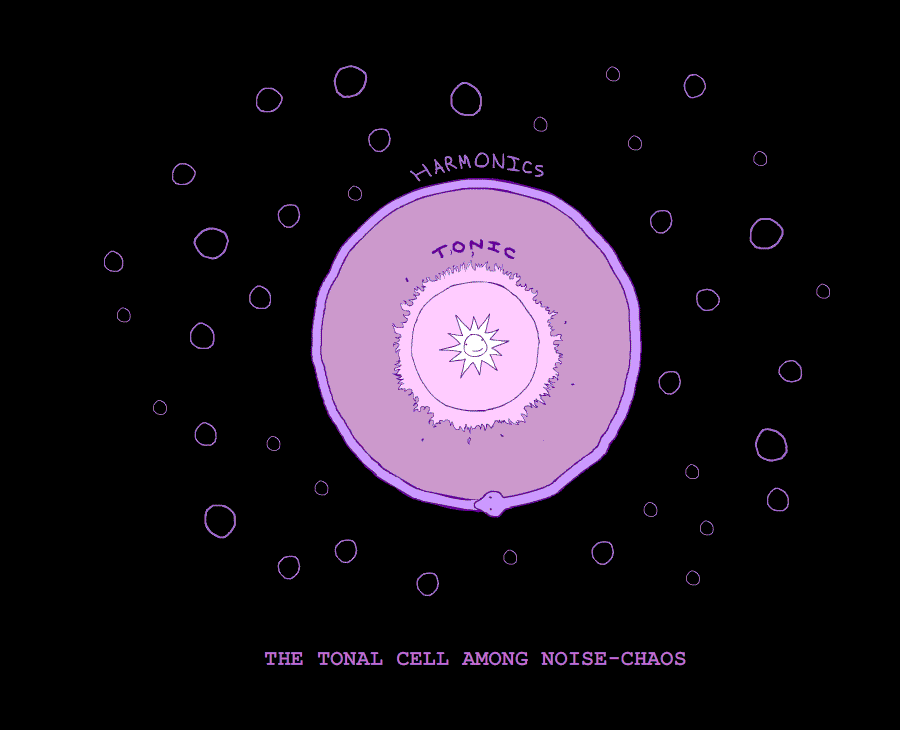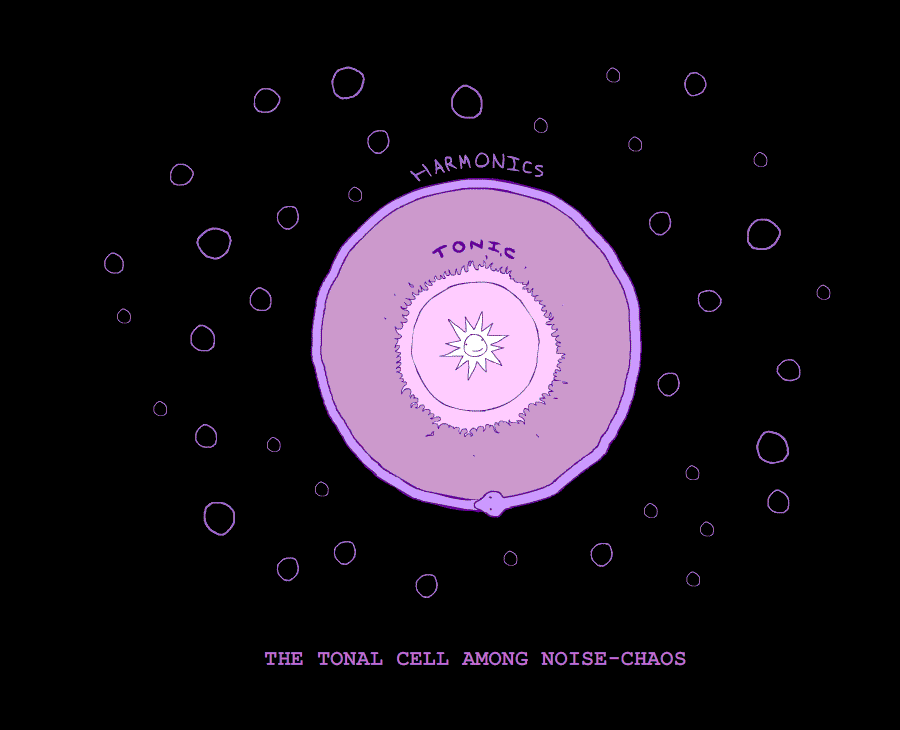
To truly appreciate the enormity of Tone and Noise within our acoustical experience, one has to actually go outside, away from the intrusion of public speakers (always growing more and more inescapable as time goes on) and to take note of the sounds which reach the ear. One will soon find that all of these sounds can be neatly categorized into either a tone or a noise. The crashing of ocean waves, the blowing of wind, the rustling of leaves, the rolling of tires along the highway, the roar of planes - these are all noises, vague blurs of pitchless sound. The singing bird, the chattering person, the car horn - each of these is a tone, a single fluctuating pitch buffered by a harmonic series. THIS is the world of sound in its purest, most untouched state: a constant ocean of noises from which various tonal voices rise up and dissapear. Here is sound in its natural state, before the intrusion of music. This is the acoustical environment within which our ear developed and according to which it transformed itself. There were no intervals, no perfect-fourths, no perfect-fifths, no major triads; only Tone and Noise poised in violent contrast to one another.
Even in human speech, we do not yet escape from the rigid tone-noise duality. Human speech consists of a quick fluctuation between various Tone-timbres and Noise-ranges. "Ah," "Eh," "Ee," "Oo" and "Oh" are all tonal sounds which we distinguish according to their different timbres. "Ch" "Ss" "Tuh" and "Puh" are all noises which we distinguish according to their different ranges. In speech, therefore, we witness a prototype of Harmonic progression, a sequential ordering of the two basic sound-types, and a pushing of each one to the expressive limits allowed by the human voice.
Tone and Noise, therefore, form a dichotomy which as as fundamental to the ear as that between Light and Dark is to the eye, and equally rife with spiritual meaning! Our ear is not, as theorists are so eager to believe, a cold and mechanical interval-calculator; our ear simply recognizes the basic sound-forms that it evolved alongside. It does not measure out;it recollects.
The Tone is the only sound which can be called a pure Consonance. Every sound is a collection of frequencies, but only in the Tone do these frequencies compound into a single pitch; only in the Tone do frequencies interlock so seamlessly that we fail to distinguish between them entirely. Even the octave cannot boast this level of acoustical unity. The octave is still two things - two acoustical bodies conjoined together. But the Tone is unambiguously singular. In this resolution of the many acoustical parts into one pitch-feeling, have we not discovered a sound which epitomizes what is meant by the word "Harmony?"
On the other hand, Noise is the only sound that can be called a pure Dissonance. Noise is, acoustically, just conflicting information - conflicting information which has reached such a great extent that it paradoxically "evens out," arriving at a state of pure homogeneity. This sound-state is the furthest extent of dissonance: the callous blending together of many disparate sounds into a grey, pitchless soup.
My answer to the Consonance problem is simple: Consonance is Tonality. Dissonance is Noisiness.
Consonant "chords" are possible because many tones can fit together in such a way that they create the impression of a singular tone.Many tones can be "Tone-like" in combination.
Say that a church-organist is having an off-day, and he accidentally starts the hymn by playing this chord:

Here is a true dissonance. The chord consists of 6 separate tones - 6 ENTIRELY DIFFERENT PITCHES which are all fighting for the ear's attention. Even though the tones are each consonant, in themselves, in relation to each other, they create a quasi-noise feeling.
So, quickly fixing his mistake, the organist voice-leads to a strong consonance, a towering C-major chord:

Just by slightly shifting each of these pitches, the organist has eliminated that unsettling feeling of 6 pitches fighting against each other. But why? Why do these 6 tones feel unified whereas the previous 6 tones do not? It is because, although the organist is technically still playing 6 tones, all of these tones conform to a single Harmonic Series!
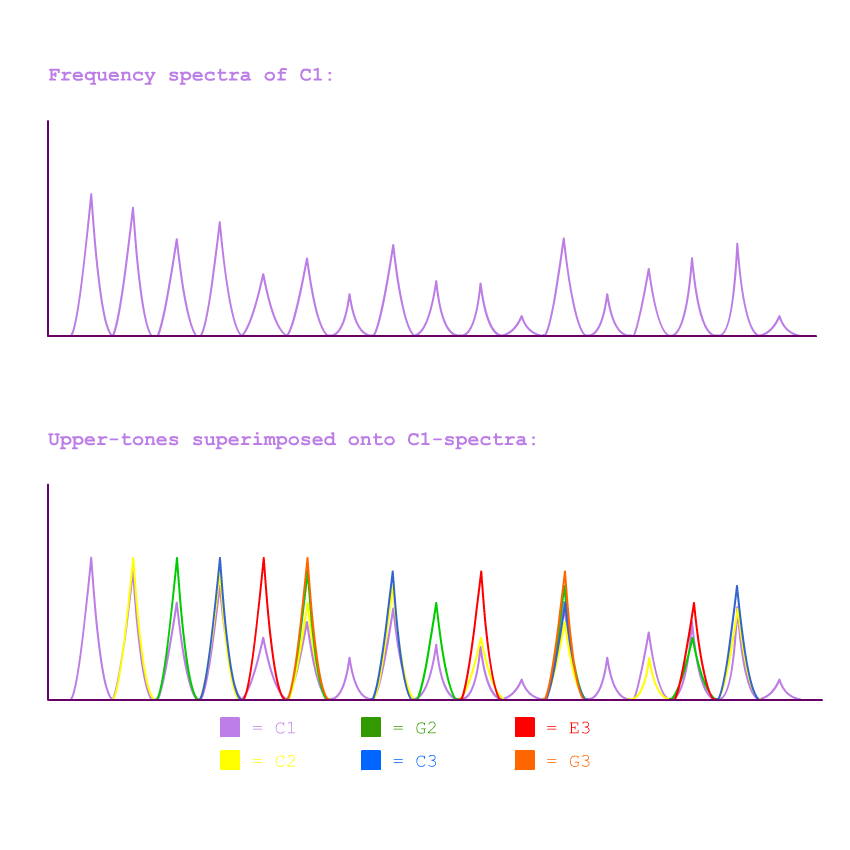
When multiple tones fall along a single Harmonic Series the resulting sound tricks the ear. Our ear recognizes not the individual tones but the over-arching Series which they fall into. As a consequence, rather than hearing 6 separate tones, we perceive a single Tone-like sound! The 6 pitches no longer conflict with each other, because each one is incorporated into the harmonic series of C1. C2, for instance, becomes the 2nd harmonic of C1's series. C5, likewise, becomes C1's 5th harmonic. Each of the 5 upper-tones is assimilated into the C1-tone. What we get, as a result, is a single network of frequencies stemming from the pitch of C1.
The most widely accepted psychoacoustical explanation for Consonance is Helmholtz's theory that Consonance is the direct result of overlapping harmonics. But this is only a half-explanation. It doesn't get to the core of what's really happening. What Helmholtz misses is the fact that whenever 2 separate harmonic series overlap with each other, they necessarily create a larger kind of meta series through their union:
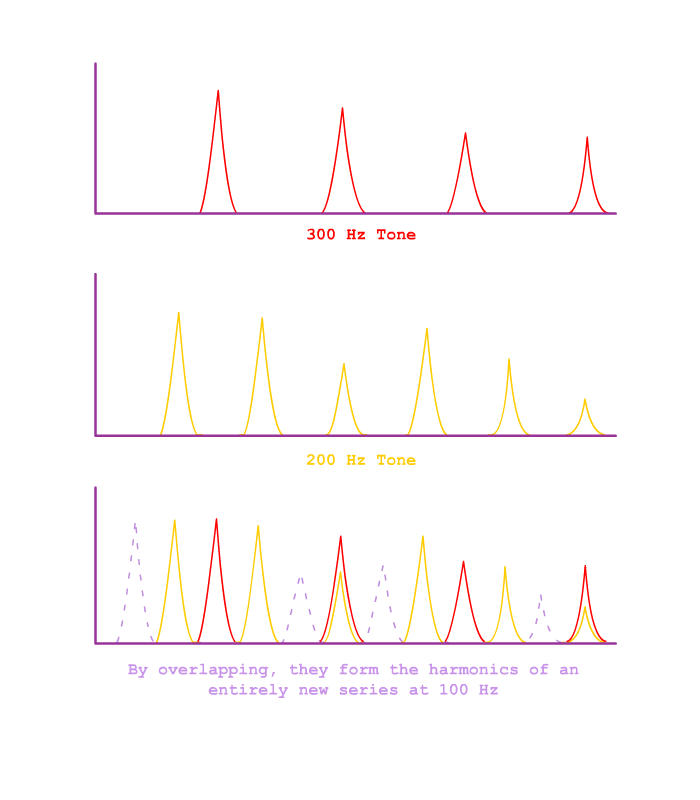
It is by virtue of this "meta" series that the tones unify. The source of consonance is not in the two actual tones, but in the overarching Tone-like sound which is created by their union.
So, Consonance is not a matter of number, but of semblance. A sound may not be a pure tone, but it might be similar enough to a tone to at least rouse our Tone-seeking ear - to make it turn its head and go "huh? wuh?" Just as a cloud which resembles a human face will naturally draw the eye, achieving distinction against the formless sea of clouds surrounging it, so too does a sound which resembles a tone naturally draw the ear, achieving distinction against a formless sea of noises. Chords and intervals can be Consonant on this very basis. The extent of any sound's consonance can be determined simply by comparing it to a pure tone. The more closely a sound resembles the Tone, the more Consonant it is; the more a sound deviates from the sound of the Tone, the more dissonant it is.
Tonality, then, is not something peculiar to Western Harmony, but a principle which is common to all styles of Harmony. Wherever one finds a Tradition of Harmony, whether it is Islamo-Indian Raga, American Jazz, or any of the thousands of locally-bound folk musics lying scattered across the globe, one will always find some elaboration upon the Tone. All sound-structure is Tonal, and the properties inherent to this structure are something which every composer must deal with, just as every architect must deal with the laws of gravity. This is a fact not consciously realized but instinctually felt by every composer, every tuner, and every performing musician. Everyone who has ever contributed to the progression of their own musical culture has, without realizing it, felt the pull of the Tone upon his ear. The sense for Tone-like sound, hammered into his psyche by millions of years of evolution, unconsiously influences every musical decision he makes, driving him to create scales, chords, progression, melodies, and songs which ground themselves in the firm structure of the Tone. For the moment he strays too greatly from this structure, he invokes Noise, and, with it, the grey and banal feeling of acoustical homogeneity.