

The Tone is the basis of all of Harmonic structure. Every sound is a collection of frequencies, but the Tone is the only one of these in which the frequencies unify into a coherent form. Consonance is Tonality.
So it should be no surprise that Harmony, in its earliest stages, takes the form of a Drone, a single tone hovering in one place. Early humans could produce the Drone by blowing into a conch shell or by vibrating their lips into a hollowed-out tree trunk. Imagine how shocking it was for man to discover something so alike to his own voice hiding within these husks of life, as if the spirits of their former inhabitants still dwelled within them. They must have held these proto-instruments up as divine vessels, as magical objects which could contain the actual spirits of the dead. And so, even in its earliest incarnation, the Tone is correctly associated with the mystical and divine. It is no coincidence that every harmonic tradition arises at first from religious ceremonies.
The spiritual feeling inherent to the Drone becomes further exaggerated in its variations: a tone which slowly fluctuates in timbre as if breathing, or a single tone which jumps up and down in pitch as if dancing.
Later on, we create more complex sounds by combining multiple tones together. But due to our unconscious bias towards the sound of the Tone - our comprehension of a feeling of unity in any sufficiently Tone-like sound - every multi-tonal structure we create ends up resembling the Tone in some way. Regardless of how greatly our harmonic progressions grow in complexity, they never fully break free from the basic structure inherent to tones. Harmony, therefore, never ceases to be anything other than heavily embellished-upon Drone music.
But to embellish is also to distort. Any alteration of a tone makes it less Tone-like and, consequently, more Noise-like. A tone with missing harmonics, a tone with a disproportionately loud 5th harmonic, a tone with a stretched harmonic series - these are all imperfect consonances. We recognize them as Tonal, but simultaneously we recognize something off in them - something strange or lopsided which tarnishes their consonant purity. And so, the more we embellish upon the Tone, the more we inevitably lean towards dissonance.
So over time, the slight fluctuation in timbre which characterizes the early Drones steadily evolves into an extreme fluctuation between Consonance and Dissonance. A progression from C major to a Diminished 7th back to C major is fundamentally just a movement from a Tone-like sound to a Noise-like sound back to a Tone-like sound:

This is the common harmonic trope of Consonance - Dissonance - Consonance. A tonal shape is established, then distorted, then reconfigured into another tonal shape roughly resembling the first one. This fluctuation between distortion and purity, between tonal destruction and tonal restortion is the central trope which the entirety of the Western musical development has been one continuous elaboration upon. All advances in Western music have consisted of finding new, more intense tonal distortions, and new ways to "resolve" these distortions back into their consonant form. The sheer intensity and drama which we find in Western music cannot be pinned on its “numerical relations” or its “logic”; rather, it is to be attributed to the deeply spiritual connotations of the Tone, and the utter violence with which our composers treat it. A dissonance is a twisting, pulling, pressing, cutting, an utter mangling of the Tone, whereas the resolution afterwards is the Tone's rebirth, its purification. In this way, a fluctuation between Consonance and Dissonance is a dreadful and exhilirating Tonal dance.
At the end of my last blogpost, I demonstrated how a major chord and a perfect fourth are Tone-like, but there may still be readers who have some difficulty imagining how my theory of Tonal likeness can possibly be applied to the whole wide range of possible harmonies. In this blog entry, therefore, I will explain some of the more complex consonances and how they are Tone-like; furthermore, I will explain how these consonances can be elaborated upon to more complex sounds which still bear the tone's resemblance. It will be shown, not only that every Harmony is a tonal elaboration, but that the extent to which we perceive each harmony as dissonant depends entirely upon the extent to which it deviates from a pure Tone.
First of all, in order to know what qualifies as a deviation from the Tone, we need to establish what a "purely Consonant" Tone is. Fundamentally, the Tone is a sound which is made up of many frequencies but only heard as one pitch. Any obscuring of this one-pitch-feeling, therefore, equals a deviation from tonal purity.
The purity of a tone's pitch-feeling depends on two qualities: the placement of its frequencies and the volume of its frequencies - harmonicity and timbre respectively.
Harmonicity refers to the actual positioning of a tone's frequencies in relation to a harmonic series. This is pretty straightforward. Naturally, the frequencies in a tone are positioned so that they are all multiples of the tonic. Any frequencies which fall out of place from these natural harmonic-positions will jut out weirdly.
Compare, for example, a tone with a regular harmonic series:
amd a tone with a "stretched" harmonic series:
Here we have a pure tone and impure tone - consonant and not-so-consonant. In the first tone, every frequency is perfectly absorbed into the tonic-pitch. In the second tone, we have difficulty telling exactly what its pitch is, as the upper-frequencies are audibly struggling against the tonic, rather than assimilating into it. The sound, then, is a semi-noise - it almost feels unified, but doesn't. It is somewhat like a tone, but also has this clangy metallic feeling to it.
On the farther end of inharmonicity, we have the tones produced by bells. Bell-tones are so easily identifiable because of the irregular harmonic series which they produce:
Every tone which is excessively inharmonic has this bell-like quality to it, and it is likely that the reason bells are so universally employed for religious ceremonies is the fascination we have with their inharmonicity.
Timbre refers to the volumes of a tone’s harmonics in relation to each other. It is not enough that a tone’s frequencies fall into one harmonic series; the volumes of these frequencies also must relate to each other in such a way that none of them obscure the tonic-pitch.
Because of the way that the Harmonic Series is naturally produced, the overwhelming majority of timbres that we hear in nature follow a common pattern: the tonic is the loudest and, as the harmonics rise in number, their volume gradually tapers off.
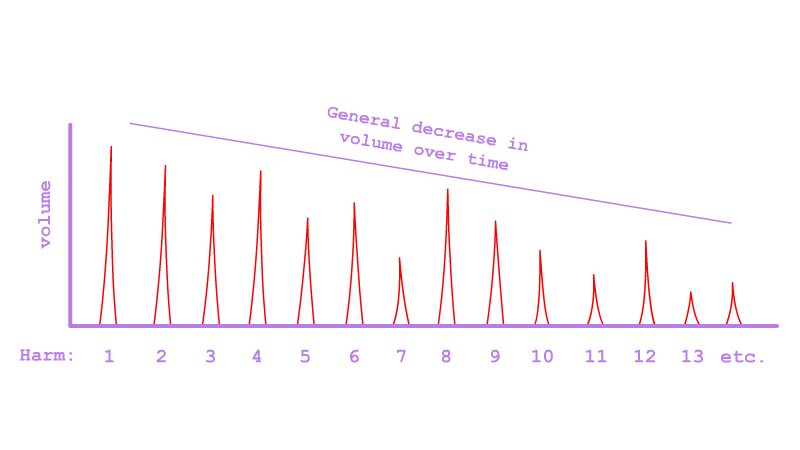
This is the normative timbre of tones. Although timbre varies greatly from tone to tone, the variance is largely constrained to this pattern. Only recently have humans learned to artificially produce tones which deviate greatly from normative timbre. But artificial is artificial. The normative timbre is that which our ear has accustomed itself to throughout millions of years of evolution; furthermore, it is the timbre of the human-voice, that tonal sound which we feel an inherent bias towards, and which ought to be considered, at least in the human ear, the purest consonance that can be reached.
So, any deviation from normative timbre is a deviation from pure consonance. Compare an oboe-tone, which has a pretty normative timbre, to an artificially produced tone which has the inverse of normative timbre, loud upper-harmonics and soft lower harmonics:
This lopsided timbre often creates a "buzzy" sound.
Here is an even greater deviation from normative timbre, where many of the lower harmonics have been completely removed:
It's the same pitch, but now that pitch is so tenuously and bizarrely expressed that we really have to strain our ears to pick up on it. Here we see that dissonance directly correlates with the "ease" of detecting a sound's underlying pitch. The more ambiguous a tone's pitch becomes, the further the tone dissolves into a noise. I think it would be absurd not to consider these dissolved tones "dissonances" in precisely the same way that we would consider tritones "dissonances"; both have that noisy, rootless feeling that occurs whenever a sound is no longer bound by a single pitch. There is such a thing, therefore, as a "dissonant timbre."
It should be noted, before we move one, that the definition I have given of normative timbre (harmonics generally decrease in volume over time) is only a very general one, which I have made brief for the sake of keeping this blogpost focused. There is much more to be said about what really constitutes a pure timbre, which harmonics are naturally soft and which are loud, and what this says about tonal structure in general. But that will have to wait for a later blogpost.
Normative Timbre and Normative harmonicity play an equal role in the purely consonant feeling of a tonal body, and any deviation from either of these two necessarily leads to dissonance. Going forward, when trying to determine the extent of a sound's Consonance or its Dissonance, we only need to compare the timbre and harmonicity of the over-arching sound to that of a pure (normative) tone.
As I demonstrated in my last blogpost, "Consonant Harmony" results from many tones coming together in such a way that they impress the feeling of a single tone. That we are distinguishing, here, between the separate tones that go into a chord and the over-arching tonal impression which is thus created demands a total reconsideration of harmonic structures.
The following consonant chord combines 4 tones in such a way that they roughly resemble a tone at the pitch of C1:

The chord is, on a superficial level, composed of 4 tones - 4 separate harmonics series, each bolstering their own particular pitch. On the other hand, these 4 series all fall into one overarching “meta” series which is the source of the chord’s unity. Within the chord, therefore, we can distinguish between two harmonic layers: the set of individual series which the chord consists of, and the broader series which they create through their union. These two layers I respectively call Sub-tonal and Meta-Tonal.
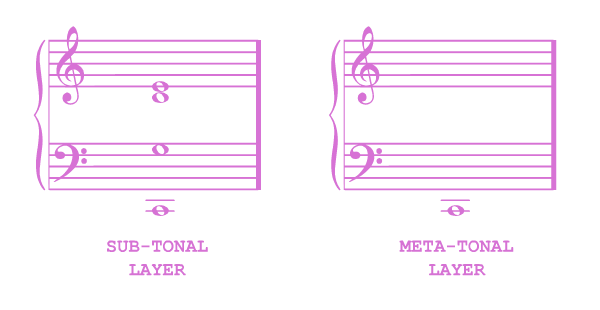
Every consonant chord is, in essence, a “meta-tone” (MT), a tonal image constructed through the union of a set of lesser “sub-tones” (ST).
Each sub-tone is an extension of a particular meta-tonal harmonic. The pitch of the E3-tone, for instance, is the same as the meta-tone's 5th harmonic. This means that the E3-tone's harmonic series, since it accentuates the pitch-feeling of E3, accentuates the 5th harmonic of C1. If we view the harmonic series as a network of interrelated frequencies, then it is as if C1's series forms the main body of this network, and the series of G2, C3, and E3 are blossoming out from different harmonic-nodes of this main body.
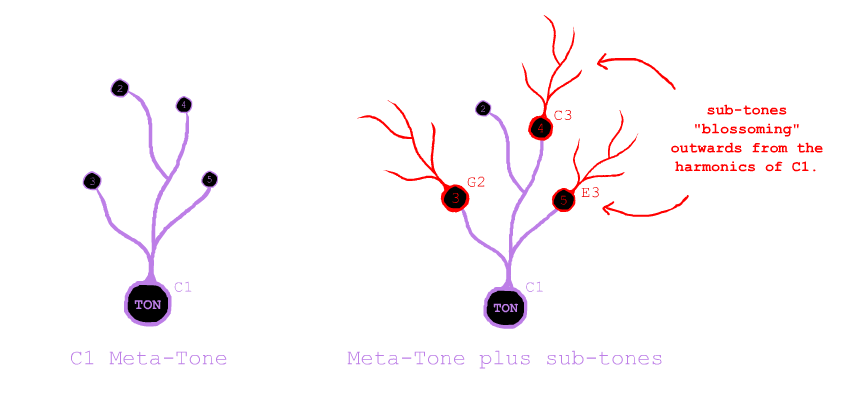
Sub-tonally, C1, G2, C3, and E3 are individuated tones, but meta-tonally, they are accentuations of different parts of the broader structure set in place by C1. Accordingly, these sub-tones can be notated ST1, ST3, ST4, and ST5 to indicate that they accentaute the 1st, 3rd, 4th, and 5th meta-harmonics. Furthermore, the entire chord can be notated as C1:[ST 1 3 4 5] to indicate that ST1, ST3, ST4, and ST5 create a meta-tone at the pitch of C1.
In this system, C1 is both the MT and ST1. This may seem a little confusing, but we have to distinguish between the overarching tonal image resembling a C1-tone (MT), and the sub-tonal C1 (ST1) which contributes to fleshing out this image. This distinction makes more sense when you remember that, even if the ST1 is withheld, the meta-tonal structure remains intact (see, virtual pitch):

To further drive home that the MT and ST1 are separate, I direct the reader's attention to the frequency spectrum of the interval which I examined at the end of the last blogpost, which can be notated, in our new language, as C1[ST 2 3]:

Remember, the entire reason that this interval is consonant is that, when the 2 harmonic series overlap, they create the series of C1. So although there is no C1 physically played, the ear still "hallucinates" a C1-tone to a certain extent. This tonal hallucination is the meta-tone.
Judging the consonance of a chord is simple; we just compare the timbre and harmonicity of the meta-tone to that of a pure tone. In the case of the C1:[ST 1 3 4 5] we find that, although its harmonicity is pure, its timbre is slightly abnormal, because ST2, ST3, and ST5 disproportionately raise the volumes of many of the upper-harmonics. So, although the chord is very consonant, it is not purely so.
Frequency spectrum of a C1-tone:
spectrum of our chord:
You can always expect a meta-timbre to be somewhat “lopsided” or “top-heavy” if we have sub-tones anywhere but the tonic. This lopsidedness is what makes all chords, by necessity, a little bit dissonant.
Observe how moving sub-tones onto higher and higher meta-harmonics gradually distorts the sound's meta-timbre more and more, intensifying the feeling of dissonance:
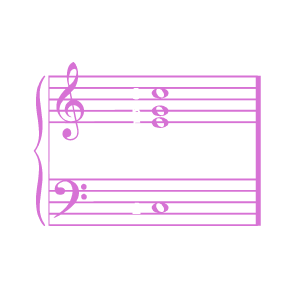


Until, as with every Tonal distortion, we reach the breaking point where the tonal image being distorted is no longer recognizable. If we only have sub-tones at 7 9 13 and 15, for instance, the timbre of the meta-tone thus produced is so abnormal that we no longer perceive any tonality in the chord at all. We have stretched the meta-timbre to its breaking point, and all we are left with is a bunch of tones - a mere noise:
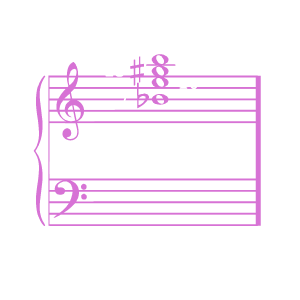
So, by changing our sub-tonal "voicings" we create different meta-timbres. "Dissonant chord voicings" happen when these meta-timbres become abnormal.
At last, we have the context and tools to create an actual harmonic progression. By constantly changing the sub-tonal voicing of a meta-tone, we fluctuate through various meta-timbres, resulting in a very safe and inoffensive harmonic progression. If you've ever listened to 1-hour ambient meditation god-frequency music on youtube, this is exactly what they’re doing:
What we call an "arpeggio" is really just playing one sub-tone at a time:
A suprising number of famous musical progressions rely upon this technique of "tracing" through a single meta-series. For instance, we have the famous opening to the William Tell overture:
The influence of timbre upon consonance can be taken advantage of here to create a kind of resolution. Moving from an abnormal meta-timbre (sub-tones at high harmonics) to a more normative meta-timbre (adding sub-tones to lower harmonics) constitues a movement from Dissonance to Consonance:
The first chord, in a purely meta-tonal sense, is an incomplete tone - a tone with the entire lower part of its series missing. The second chord fills in all of these missing parts. This is why the resolution sounds so satisfying: the restoration of an incomplete tonal structure. Moreover, because the first chord implies a tonal structure, and the second chord blatantly affirms it, we are validating an assumption made by the ear.
Chopin LOVED this type of resolution. The final bars of his pieces were almost always like this: he would play sub-tones in the middle-range, then sub-tones way up high, and finally, he would land on ST1 and ST2 (this interval is almost indistinguishable from a pure tone, so he's really just landing on a beefier version of a pure tone):
No theory of Harmony other than mine offers an explanation for resolutions like these. How can we resolve from the tonic to the tonic, Rameau? How can we resolve from a I-chord to a I-chord, Hugo Reimann? How can we resolve from less tones onto more tones, Harry Partch? The answer is: intervals don’t matter; roman numerals don't matter; only Tonal resemblance matters!
The second way we can distort a meta-tone is harmonically - that is, by displacing its harmonics from their natural places in the harmonic series, thereby corrupting the structure.
For instance, let's take a fairly strong consonance, C1:[ST 2 3 4 5], and then detune ST5 slightly upwards:

By pulling the ST5 slightly away from its natural position in the meta-tonal structure, we add some "potential energy" to the harmony. The ST5 is a stretched out rubber-band that we naturally want to snap back into place. When it actually does, in the third chord, we almost feel relief.
Whereas, at the beginning of the progression, ST5 is hidden away in the consonant embrace of the meta-tone, when we displace it from its position in the harmonic series, it protrudes like a jagged edge. When ST5 is retuned back to its original place, it sinks back into the warm body of sound from which it had departed. So, there is an establishment of a tonal form, a distortion of that form which creates a feeling of tension, and finally a restoration of the form which satisfies that tension. This creation-tension-fulfillment formula has been central to Western music for about a millenium. Overall the "tension" part of this progression is so mild and brief that it actually feels quite pleasurable... like a tonal massage.
But what about a harsher dissonance? What if we displace ALL of the sub-tones?
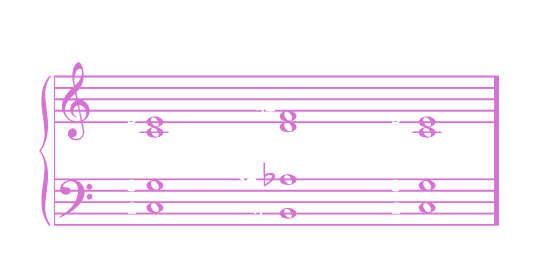
Here, we really blur the line between what is "Tone-like" and what is "Noise-like." Whereas, in the previous example, most of the tonal structure is left alone, here it is utterly mangled. Here is where we get that feeling of pain or displeasure which is often ascribed to harsh dissonances, where “tonal massage” crosses over to “tonal torture.” One can almost hear the Tone screaming out in pain as its harmonic-limbs are stretched and pulled into the most unnatural positions, forced into an excruciatingly Noise-like sound. But the intensity of this dissonance only amplifies the relief we feel when the harmony resolves
But, going back to the previous example, instead of moving the ST5 up a little, stopping, and then moving it back down, we can actually keep moving it upwards until it hits the 6th meta-harmonic, turning it into ST6!
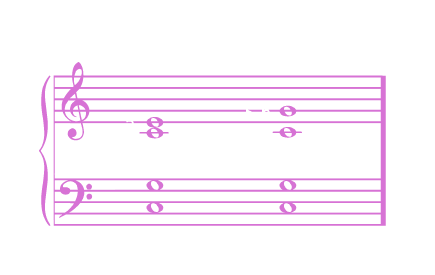
While the sub-tone is moving between ST5 and ST6, as is as if it is being torn between the gravitational pull of the 2 meta-harmonics.
While ST5 is shifting to ST6, we can shift ST4 to ST5:
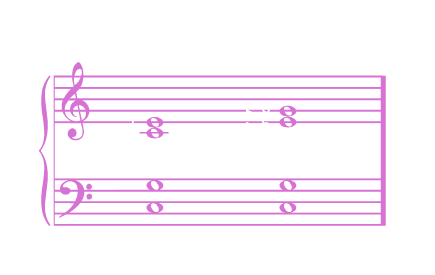
And you can just keep doing this - traveling from meta-harmonic to meta-harmonic over and over to create a decent chord progression:
Of course, due to the limitations of our 12-tone intruments, we cannot freely glide between these different harmonics in practice. If we transcribe the progression above to piano, we get a "bitcrushed" version of the harmony:
The opening of Beethoven's piano sonata in F# is like this:
See? Beethoven even leaves the ST1 and ST2 down below at all times just to cement the meta-tonal feeling. Because that ST1 and ST2 are always there, the progression is warm and unambiguous; there is never a point where the meta-tonal identity comes into question. Meanwhile, the upper-tones are slowly crawling upwards, occasionally locking into different points of the meta-tonal structure. The meta-tone gradually expands outwards, ultimately growing from one consonance - SUB 1, 2, 4, 5, 6 - into a broader one - SUB 1, 2, 8, 12.
If we actually remove the ST1 and ST2, the progression remain tonally comprehensible. Thought the ST1 (the meta-tonic) is not actually played, we still feel its pitch all the way throughout:
These progressions are still just elaborations upon the Drone. The harmony is still, at its core, a single tone fluctuating in timbre. The only difference is that, now, our timbre is far more variable, because it consists of many sub-tonal parts which can be moved around independently.
One of the weirder Harmonic phenomena that music theorists always seem to stealthily ignore is the nature of melody; specifically, why the top note of a chord always seems to draw the ear. But if we treat chords as meta-tones, a simple explanation arises.
Remember, we are used to hearing tones at a normative timbre where the harmonics gradually decreases in volume as the harmonics get higher. But this means that if a very high harmonic - say, the 10th harmonic - is about the same volume as the tonic, then it will be heard disproportionately loud - that is, it will stand out.
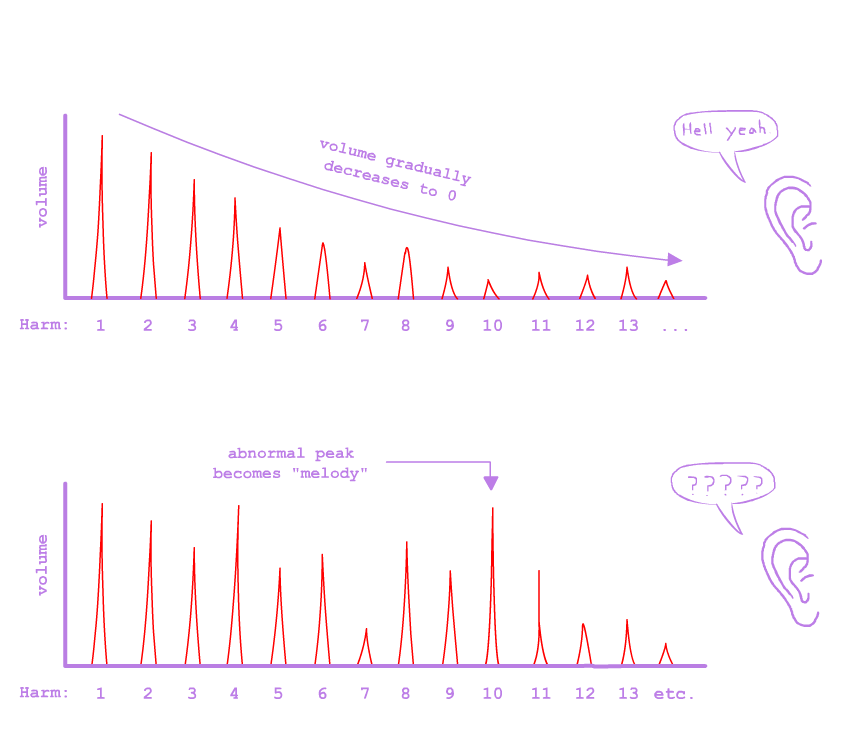
That’s why, in all of the chord progressions we’ve done, the pitch of the highest tone is always the most clearly audible. Assuming that all the sub-tones in a chord are played at the same volume, our ear will always be drawn to the pitch of the highest one, because that is always the most disproportionately loud frequency in the entire structure. This is my explanation for why melodies draw the ear. If any other theoretical system has some valid explanation for melody, I have missed it.
Just like before, let’s take a C1 Meta-tone and displace its sub-tones. Let's say the meta-tone C1:[ST 2 4 5 6], and we detune both ST5 and ST3 upwards:

Wait, something is different about the chord we moved onto. Just like before, we've distorted the Meta-tone of C1, so why does the second chord sound so much more structurally firm than our other examples? Well, this time the second chord is not just a distortion; it also forms an entirely new tonal shape, a meta-tone at F0!
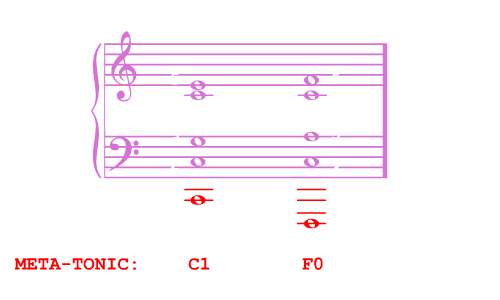
A kind of harmonic "pun" is happening here. The second chord can either be heard as a distorted version of the first meta-tone - C1:[ST 2 3+ 4 5+] or as a different meta-tone - F0:[ST 3 5 6 8]. In reality, both of these harmonic possibilities weight on the ear simultaneously. "Have we distorted the C1 or have we resolved onto the F0? Which is the consonance and which is the dissonance?" It is only when we move back to a C1-chord that this harmonic ambiguity is resolved. It is as if the composer says “Nah just kidding. It was a C1-drone the whole time.”
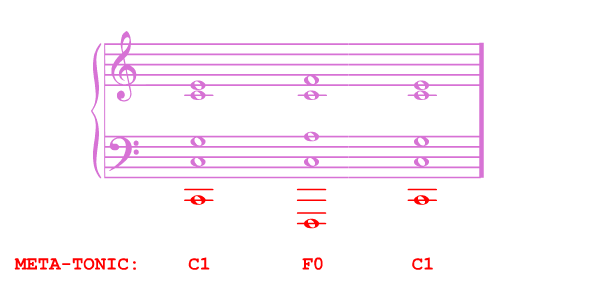
Like all double-meanings, this harmonic technique adds something akin to depth to our work. Harmonics are acoustical colors. The 1st, 2nd, 3rd, 5th, 7th harmonics bear contrasting acoustical feelings on par with the contrasting visual feelings of red, yellow, blue, green, and violet. Because the second chord bears the shade of two harmonic series, each sub-tone within the chord is "dual-colored." The lowest tone, for instance, is both the ST2+ of C1 and the ST3 of F0. The top tone is both the ST5+ of C1 and the ST8 of F0. This "meta-tonal pun," then, not only adds an exciting layer of ambiguity to our artform, but also, by juxtaposing multiple meta-tonal series, enriches the palette of the composer. Whereas before he only worked with the basic harmonic-colors given to him by the harmonic series, now he can freely mix these together to get every hue on the spectrum.
Good Harmony is rich with these double- triple- quadruple meanings. Composers are constantly juggling around various meta-tonal feelings, deciding on a whim whether they should resolve onto a certain one or continue to string the listener along. And yet, even with all this added harmonic depth, the progression is still just a C1-drone. Every single frequency which makes up the progression is heard in direct relation to the pitch of C1. Every chord still receives the hue of C1’s harmonic series. The meta-tonal feeling of F0 only applies to the second chord. We must acknowledge this added layer of structural depth. In addition to the Meta-tonal/Sub-tonal distinction, therefore, I distinguish between the primary meta-tonal structure which is heard throughout the whole progression and the secondary meta-tonal structure which appears only briefly. I call the latter a regular meta-tone (MT) and the former the meta-meta-tone(MMT). Applying this distinction, we get the following analysis:
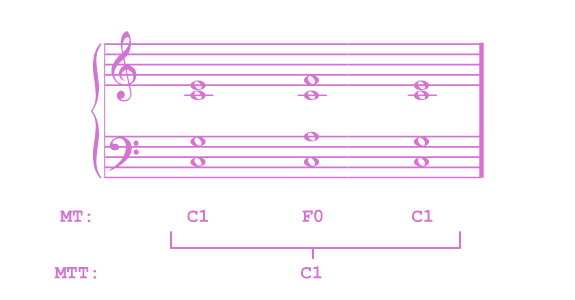
Observe the following chorale, in which many MTs are touched upon, but in which there is still a constant MMT of C1:
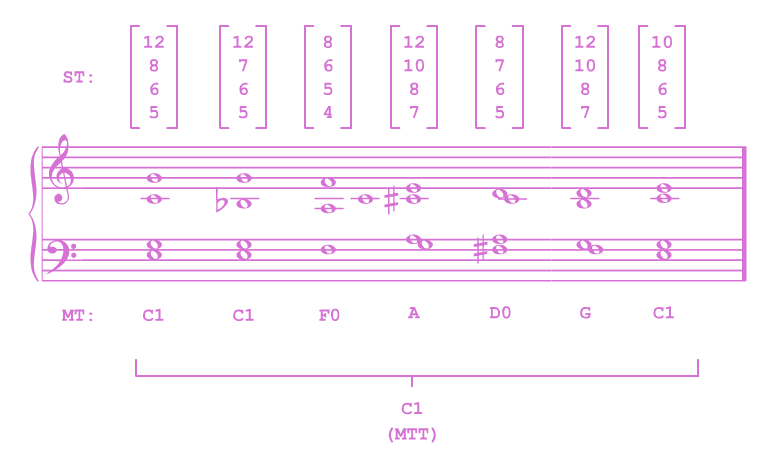
On the MMT layer, we hear a single C1-chord warping over and over before finally resolving back onto a consonant shape. But, every time the C1-chord warps, it does so onto a new MT: first onto F, then onto A, then D, then G, then back onto C. The harmony is constantly transforming and renewing into different tone-like shapes, but these shapes are always heard against the backdrop of C1’s Harmonic Series. Every sub-tone stands both in relation to its own tonal cell, and to the broader C1-structure which encompasses the whole of the Harmony.
Now, there is probably a reader or two who, being overwhelmed by the new , is now absolutely sure that I am jumping through mental hoops in order to justify the conclusions which I established in the last blogpost, and that this “meta-meta-tonal” layer is total cope. To counter such readers, I would first point out that the progression never feels fully resolved up until the final chord, when the MT matches the MMT. Second, observe how it sounds when the ST1 of the MMT layer, C1, is sounded throughout the whole progression:

The C1-tone doesn’t clash with the progression as you might expect it to; rather, it seems to form a perfectly solid foundation upon which the upper-chords dance. This is because C1 is the ST1 of our MMT. By playing it underneath the progression, we are just blatantly affirming what is already imagined by the listener.