

In my previous blogpost, I put forward a theory of Consonance which is really less of a harmonic system than it is a simple analogy: consonances are Tone-like and dissonances are Noise-like. This analogy is the basis upon which my music theory rests. For a sound to be consonant, it just has to roughly resemble a Tone.
If acoustical structure only comes about Tonally, then the widely spanning set of harmonic shapes that we hear in music is nothing more than a set of Tonal embellishments. Just as we can regard the entire history of portraiture as a continuous elaboration upon man's image, so too should we regard the entire history of Harmonic progression as a continuous elaboration upon the sound of the Tone, within which there is always the implicit suggestion of the human voice: man's acoustical image. In both cases, every embellishment upon the image draws out some deeper feeling; the set of embellishments in their totality contribute to what we might call a style. The sum-whole of a cultural style can be defined as the particular way that it chooses to elaborate upon the Tone.
But every embellishment is a distortion. The more we transform a tone, the more we inevitably reshape it into something else - into something which is not a noise, but which is also not quite a tone. Take, for instance, if we were to detune a few of a tone’s harmonics.
We perceive a tonal sound, but simultaneously recognize that there is something off about it. It might be a tone, just like that face you caught a glimpse of in the darkness at night might be an actual face. But, also, what is wrong with it? Here, precisely is the source of both dissonance and the feelings of amiguity, strangeness, harshness, and violence which belong with it. Every dissonant harmony is a distorted Tone.
The fluctuation between Consonance and Dissonance, therefore, is just a constant distortion and reshaping of the Tone. Harmonic progression, at its core, is dream-like fluctuation between many Tone-like shapes.
In this blogpost, I will discuss many of the conventional shapes that we see in Harmony and show how they are essentially just Tonal embellishments which can sometimes lean towards intense dissonance.
Every consonant chord is Tone-like. Although many separate tones go into the making of a chord, they combine in such a way that they impress the feeling of a single tone upon the listener.
Say that a church-organist is having an off-day, and he accidentally starts the hymn by playing a pretty harsh dissonance:

In this sound we hear 6 separate tones, 6 pitches all fighting for the ear's attention. This is an acoustical clutter and, consequently, belongs with Noise.
So, quickly fixing his mistake, the organist shifts each voice slightly changing the chord to a powerful consonance - a towering C-major chord:

Just by slightly shifting each of these pitches, the organist has eliminated that unsettling feeling of 6 pitches fighting against each other. But why? Why do these 6 tones feel unified whereas the previous 6 tones do not? It is because, although the organist is technically still playing 6 tones, all of these tones conform to a single Harmonic Series.
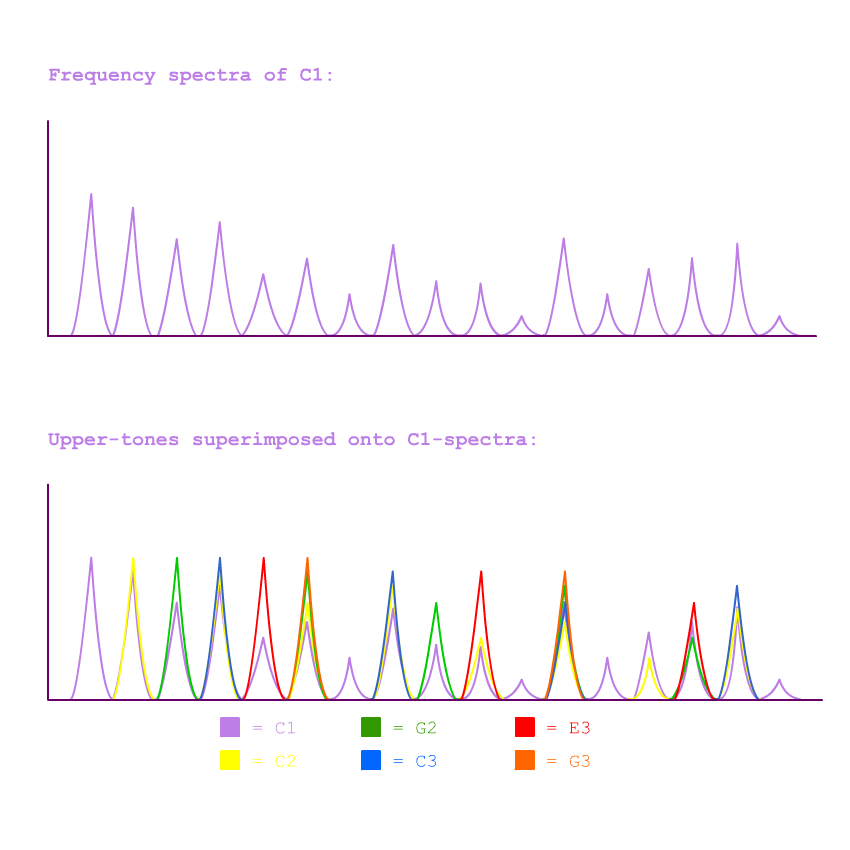
So, although there are technically 6 tones sounded, our ear immediately comprehends, not the separate tones, but the over-arching Harmonic Series which they fall into. It doesn't matter how many tones we INTEND to play; as far as our tone-whore of an ear is concerned, when many frequencies conform to a single harmonic series, they are ONE tonal sound.
But, does all this sound ridiculous to you? Is "many tones creating the impression of one tone" just a bit of sophistry I have conjured up to push my theory? I would ask the reader: on what basis do we call the chord above "6 tones?" Just because something is written as 6 notes, and the organist hits 6 keys on the organ, does that necessarily mean our ear will recognize the sound as such? If our goal is to understand the world of acoustical phenomena, then we need to appreciate how great the discrepancy often is between music as it written and music as it is actually heard. Written music is, after all, just a guide for the performer to play his instrument correctly. But the moment these inked notes are played, they become something entirely new; they become ACTUAL SOUND. We music theorists should take care to study this actual sound, and not the notes which represent it.
When we begin to truly listen, it becomes obvious how blurred the line is between monophony and homophony. Compare, for instance, a single tone and an octave:
Here is a C1-tone:
And here is a C1-tone and a C2-tone played simultaneously (an octave interval):
Sound-wise, the two are nearly identical. It almost feels like, instead of adding another tone, we just changed the timbre of the initial tone. Indeed, an octave can easily be confused for a single note, if you aren't already accustomed to what a "single note" is supposed to sound like on a particular instrument. THAT is consonance. THAT is what it means for a sound to be Tone-like. It means that, although a "single tone" and an "octave" are easily distinguishable on paper, in terms of ACTUAL SOUND, the distinction between the two is barely even real.
There is a well-known phenomenon among acousticians called "phantom pitch." Basically, even if you take away a tone's tonic-frequency (its 1st harmonic), we will still hear the tone at the pitch of that tonic.
Here's a pure Tone:
Now here's that same tone with its tonic removed.
The pitch remains the same, despite no such frequency representing that pitch. This phenomenon only affirms what we have discussed: that a tone's pitch is an acoustical feeling created not just by its tonic, but collectively by its entire series of harmonics. The entirety of the Harmonic Series - not any particular frequency - bolsters the pitch-feeling. Naturally then, removing any single harmonic from a tone, even one as important as the tonic, will not cancel this feeling out, but will only slightly weaken it.
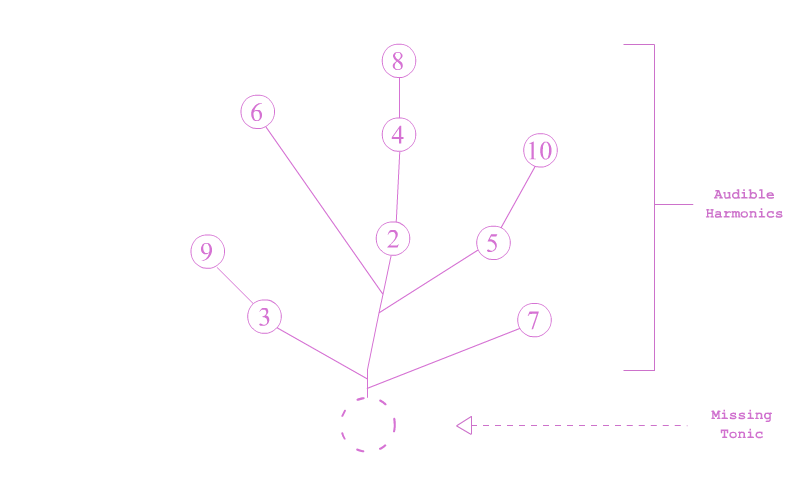
What is remarkable is just how many harmonics we can take away from a tone before its pitch-feeling begins to noticably disintegrate.
Here is what happens when we remove the 1st - 4th harmonics:
And the 1st - 8th harmonics:
But phantom-pitch has its limits. The more of the harmonic series we remove, the more vague the pitch-feeling becomes.
If we only leave the 6th, 7th, and 11th harmonics of the previous tone, for instance, we can still just barely hear that underlying pitch, but we have to really strain our ear to do so:
And finally, if we only leave the 9th and the 13th harmonics, it becomes impossible to hear the pitch. Each harmonic removed is a brick pulled from the over-arching tonal structure until, at some crucial point, everything collapses, and all we are left with is a jumbled heap of Noise.
But all of this is to say that, within certain limits, even FRAGMENTS of tonal structures will be heard as consonant. The removal of harmonics is, itself, a kind of tonal embellishment which, in greater degrees, leads to intense dissonance.
We have discussed two kinds of tonal embellishment:
1. Additive (adding a tone which falls into the initial tone's series)
2. Subtractive (taking away harmonics)
Combining these two ways of embellishing upon a single Tone, we attain every possible chord-voicing.
Here is a consonant chord:

Here is the same chord with the C1-tone (the meta-tone) taken away:
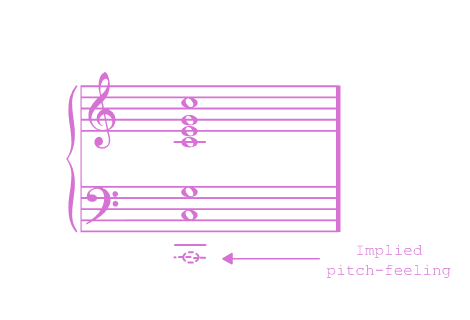
For instance, the major triad and all of its inversions:
At the farthest extent of the subtractive embellishment, we eventually get two-tone voicings - that is, consonant intervals.
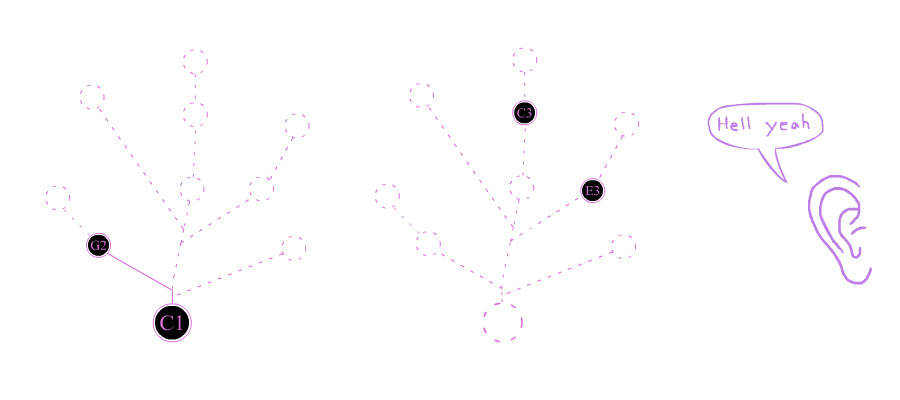
A perfect-fourth and the series it implies:
We do not hear the sound above as a "4/3 ratio," as such, but as the 3rd and 4th sub-tones of a meta-tone at 100 Hz. This is an important nuance. It is never the intervals, themselves, which are consonant, but the overarching meta-tonal structures which they imply.
The most widely accepted psychoacoustical explanation for Consonance is Helmholtz's theory that two tones are consonant with each other because of their overlapping harmonic series. Dissonance, according to Helmholtz, is the direct result of harmonics from different series beating with each other. Overlapping harmonics mitigates this beating and, hence, mitigates dissonance. But this is only a half-explanation. It doesn't get to the core of what's really happening. Helmholtz misses the fact that whenever 2 separate harmonic series overlap with each other they necessarily create a larger, more fundamental (meta) series through their union:

It is by virtue of this fundamental series that the tones are bound together; it is THIS series which is the source of thier consonance. So it is not just that the two tones are "consonant with each other"; they literally become one tone!
Playing a C1-tone after the perfect-fourth sounds like a resolution because it fills in the blank spaces implied by the interval. Before, the meta-tonic was implied; now it is blatantly affirmed. This is, itself, a kind of resolution:
It is not the intervals themselves which are consonant, but the over-arching tonal structures which they imply through their union. The ear doesn't recognize "intervals"; it only recognizes Tone-like sounds and Noise-like sounds. If an interval CAN be rationalized as part of a larger tonal body, then it will be heard as consonant; if not, it will be heard as two conflicting pitches. To recognize any interval as consonant without acknowledging its place in a larger tonal structure is to completely misunderstand the interval.
Certain intervals feel more dissonant because they are more tonally ambiguous.
A perfect 12th is a very straightforward consonance, very clearly fitting into the 1st and 3rd harmonics of a series. A major third is slightly less so, but still easily comprehensible as the 4th and 5th harmonics.
An interval of 10/9 though??? Now THIS is where our inner-ear starts to short-circuit. The thing is, an interval of 10/9 is similiar enough to both 8/9 and 10/11 to be easily confused for either of the two. Our ear is built to detect tonal structure; not minute differences in intervallic lengths. So, the ear, caught between the vertigo of these 3 separate harmonic possibilities, is unable to fully rationalize the 10/9 interval. We just end up hearing it as two separate tones.
But the intense tonal ambiguity of this interval only makes its resolution more satisfying.
What we call "Timbre" and what we call "chord-voicing" both refer to the expression of a Harmonic Series through the volume of its harmonics. The distinction between them is as arbitrary as the distinction between Tone and chord.